Tempo e Sincronização

Tempo

Num sistema centralizado não existe ambiguidade quanto ao tempo. Quando um processo A pretende saber o tempo atual, pode consultar o relógio do sistema. Se momentos mais tarde o processo B obtiver o tempo, este será superior (ou possivelmente igual) ao tempo obtido pelo processo A.

Num sistema distribuído o problema é mais complexo. Não existe tempo global, cada computador tem o seu próprio relógio e o tempo que estes relógios indicam pode ser diferente.

Relógios Físicos

Praticamente todos os computadores têm um circuito para contar o tempo, baseados num cristal de quartzo. Este cristal oscila a uma frequência conhecida, e o circuito conta o número de oscilações, podendo assim determinar o tempo. Ao fim de um determinado número de oscilações, o circuito gera uma interrupção a que se chama tick de relógio.

Como qualquer outra medição, existe uma incerteza associada à frequência do cristal, e por isso a frequência de ticks de relógio pode variar entre relógios. Mesmo para o mesmo relógio, a frequência pode variar com fatores externos como a temperatura. A variação é normalmente pequena, mas o erro acumulado pode levar a que dois relógios apresentem uma diferença significativa no tempo que contam.

Tempo Universal Coordenado (UTC)

Dada esta incerteza, surge a necessidade de um tempo universal, que sirva de referência para todos os relógios. Para tal, o International Time Bureau (BIH) recolhe medições de 450 relógios atómicos (capazes de uma precisão extremamente superior à dos relógios de quartzo) em 80 laboratórios distintos e calcula o tempo médio. Esta medição é o Tempo Atómico Internacional (TAI).

Por mais preciso que o TAI seja, não tem em conta o desvio da hora solar, pelo que um segundo standard foi criado, baseado no TAI mas incluindo leap seconds, o Tempo Universal Coordenado (UTC). Vários satélites transmitem UTC, sendo possível obter precisões na ordem dos nanosegundos.

Métricas de Desempenho de Relógios

Com uma referência externa, pode-se definir métricas para avaliar o desempenho de relógios. Para as definir, temos que $t$ é o tempo UTC e $C_p(t)$ é o tempo contado pelo relógio $p$ no instante $t$.

O skew é a diferença entre o tempo contado por dois relógios, ou seja:

A deriva do relógio é a taxa a que um dado relógio se afasta do tempo de referência:

Para um relógio perfeito, $drift\_rate(p) = 1$. Por norma, fabricantes de relógios garantem um desvio máximo. Ou seja, para um desvio máximo $\rho$:

Diz-se que um relógio está correto quando o seu drift rate respeita a especificação do fabricante. Esta condição impede saltos no tempo, porém, tal nem sempre é desejável. Uma condição mais flexível é a de monotonia, que impede que o relógio retroceda no tempo:

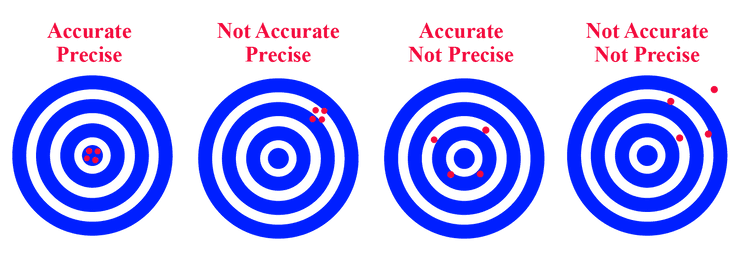
Para conjuntos de relógios, pode-se ainda falar de precisão e exatidão.

A precisão é a medida da dispersão das medições dos vários relógios. Para uma precisão $\pi$, temos que a diferença entre quaisquer dois relógios nunca excede $\pi$, ou seja:

Por outro lado, a exatidão é a medida da diferença do conjunto de relógios com uma referência externa. Para uma exatidão $\alpha$, temos que a diferença entre qualquer relógio e o tempo de referência nunca excede $\alpha$, ou seja:

Sincronização de Relógios Físicos

Num sistema distribuído em que uma das máquinas está instalada com um recetor de UTC, pode-se usar este relógio como referência para sincronizar os outros. Trata-se de sincronização externa, em que é usada uma referência externa para obter exatidão e precisão no sistema.

Porém, a exatidão nem sempre é relevante, sendo mais importante a precisão para que todos os nós do sistema concordem sobre o tempo. Nestes casos usa-se sincronização interna, em que os relógios são sincronizados entre si.

Algoritmo de Cristian

O Algoritmo de Cristian é um algoritmo de sincronização externa que usa um servidor de tempo.

O processo $p$ envia uma mensagem $m_1$ ao servidor de tempo $S$ e espera pela resposta $m_2$, que inclui $C_S(t_{S,m_2})$, com $t_{S,m_2}$ sendo o momento em que a resposta $m_2$ sai de $S$.

O processo $p$ não pode usar o tempo incluído na mensagem $m_2$, pois estaria a desprezar o tempo de transmissão. Assim, $p$ mede o $RTT$ e, assumindo que o tempo de transmissão de $p$ para $S$ é igual ao de $S$ para $p$, estima o tempo atual como:

Caso o ajuste de tempo requira um avanço no tempo, ocorre diretamente. No entanto, se for necessário um retrocesso, de modo a não se violar a monotonia com um salto para trás, a frequência de clock ticks é reduzida, até o tempo estimado ser alcançado.

É importanto notar que não é garantido simetria no tempo de transmissão, pelo que a estimativa do tempo tem alguma incerteza. No pior caso, em que uma das mensagens é enviada instantaneamente mas a resposta demora $RTT$, o tempo estimado estará errado por $\frac{RTT}{2}$. A precisão deste algoritmo é, portanto, $\frac{RTT}{2}$.

Pode-se melhorar a precisão caso se conheça o tempo mínimo de transmissão, ficando $\frac{RTT - RTT_{min}}{2}$.

Este algoritmo é simples, no entanto, tem um único ponto de falha. Se o servidor de tempo falhar, o sistema não consegue sincronizar os relógios. Cristian propõe que o pedido seja feito em multicast a vários servidores de tempo, selecionando o que responder primeiro, resultando na melhor precisão.

Algoritmo de Berkeley

O Algoritmo de Berkeley é um algoritmo de sincronização interna. Por simplicidade, o exemplo será dado para um sistema com 3 processos, o processo coordenador $C$ e os processos $p$ e $q$, mas o algoritmo pode ser estendido a qualquer número de processos.

Neste algoritmo, é eleito um coordenador $C$, responsável por periodicamente envir pedidos a todos os outros processos, que devem responder com o seu tempo.

O coordenador recebe as respostas $m_2$ e $m_4$ e calcula a média dos tempos, incluindo o próprio:

O coordenador calcula a diferença entre o tempo médio e o tempo de cada processo e envia a diferença para que os processos ajustem o seu relógio. As diferenças podem ser positivas ou negativas e são calculadas da seguinte forma:

Cada processo ajusta o seu relógio, de acordo com a diferença recebida.

O algoritmo apresentado foi simplificado, na versão real é tido em conta o tempo de transmissão, da forma como foi feito no Algoritmo de Cristian.

Em caso de falha do coordenador, um novo coordenador é eleito. Falar-se-á de eleições na próxima publicação.

Network Time Protocol (NTP)

Tanto o Algoritmo de Cristian como o Algoritmo de Berkeley são algoritmos desenhados para operar em intranets. O NTP define um protocolo distribuir informação de tempo através da internet.

Os objetivos de desenho do NTP são:

• Prestar um serviço que permita que os clientes na Internet sejam sincronizados com precisão com o UTC.
• Prestar um serviço confiável que possa sobreviver a longos períodos de perda de conectividade.
• Permitir que os clientes se resincronizem com frequência suficiente para compensar as taxas de desvio encontradas na maioria dos computadores.
• Proteger contra interferências com o serviço de tempo, quer sejam intencionais ou acidentais.

O protocolo NTP baseia-se no Algoritmo de Cristian, mas em vez apenas medir o $RTT$, registam-se os valores reportados por $p$ para o envio de $m_1$ e recepção de $m_2$, $C_p(t_{p,m_1})$ e $C_p(t_{p,m_2})$, e os valores reportados por $q$ para a recepção de $m_1$ e envio de $m_2$, $C_q(t_{q,m_1})$ e $C_q(t_{q,m_2})$.

Calcula-se a diferença entre os tempos reportados entre o envio e recepção de cada mensagem:

Podemos, por fim, calcular a diferença dos deltas para obter o offset $\theta$ e a média para obter o delay $\delta$:

O offset é uma estimativa do $skew(p,q)$ com incerteza de $\frac{\delta}{2}$. Quanto menor o delay, melhor a estimativa. O algoritmo armazena os últimos 8 pares $(\theta, \delta)$, escolhendo de entre estes o par com o menor $\delta$ de forma a obter o $\theta$ mais preciso. Este valor é então usado para ajustar o relógio de $p$:

O protocolo NTP pode funcionar em 3 modos:

• Multicast: O procedimento descrito anteriormente não se aplica e simplesmente é enviado o tempo atual em multicast para todos os clientes. Só se deve usar este modo em LANs de alta velocidade.
• Chamada a procedimento: O protocolo decorre de acordo com o descrito anteriormente.
• Simétrico: O protocolo decorre de acordo com o descrito anteriormente, mas a sincronização é feita em ambos os sentidos.

Aplicar NTP de forma simétrica implica que não só $p$ afeta o relógio de $q$, como também $q$ afeta o relógio de $p$. Isto pode causar problemas, caso um dos relógios seja mais exato que o outro. Para resolver este problema, o NTP divide as máquinas em níveis (ou strata):

• Uma máquina de nível 1 é um servidor com um relógio de referência, como é o caso de um computador instalado com um receptor de UTC.
• Uma máquina de nível 2 sincroniza com uma máquina de nível 1.
• Uma máquina de nível 3 sincroniza com uma máquina de nível 2, etc...

Uma máquina só ajusta o seu relógio com uma máquina de nível inferior.

help pls

Honestamente, não fiquei com grande intuição sobre como é que o NTP funciona. Se estás a ler isto e tens uma explicação melhor, que transmita intuição sobre o protocolo e não seja só debitar fórmulas, por favor, diz-me algo no discord.

- Luís

Eventos e Relógios Lógicos

Nem sempre é necessário contar o tempo de forma exata. Se dois processos não interagem, a falta de sincronização não pode ser observada, pelo que não poderá causar problemas. Para além disso, em muitos casos, o que realmente é relevante é a ordem em que eventos ocorrem e não o tempo absoluto.

Trata-se de um evento qualquer operação que transforma o estado do processo. Para além de alterações de estado, a recepção $recv(m)$ e o envio $send(m)$ de qualquer mensagem $m$ também são eventos.

Num só processo $p_i$, é trivial determinar a ordem em que eventos ocorrem. Diz-se que $e$ antecede $e'$ no processo $p_i$ se $e$ é obsevado por $p_i$ antes de $e'$. Esta relação pode ser representada por $e \rightarrow_i e'$.

Exemplo

Algumas relações de antecedência em $p_i$ encontradas no diagrama:

• $a \rightarrow_0 b$
• $h \rightarrow_1 i$
• $k \rightarrow_2 m$
• $b \rightarrow_0 f$

Em sistemas distribuídos, expande-se a definição de happens-before para incluir transmissões de mensagens. Diz-se que $e$ antecede $e'$ se antecede em algum processo ou se correspondem ao envio e recepção de uma mesma mensagem. Para além disso, antecedência é transitiva.

• HB1: Se $\exists{p_i}: e \rightarrow_i e'$, então $e \rightarrow e'$.
• HB2: Se $\exists{m}: e = send(m) \wedge e' = recv(m)$, então $e \rightarrow e'$.
• HB3: Se $e \rightarrow e' \wedge e' \rightarrow e''$, então $e \rightarrow e''$.

Com estas definições, observa-se que para uma sequência de eventos $e_i, i = 0..N$, se for possível aplicar HB1 ou HB2 a qualquer par de eventos $(e_i, e_{i+1})$, então, por HB3, $e_0 \rightarrow e_N$.

Nem todos os eventos têm uma ordem de antecedência definida. Diz-se que eventos distintos $e$, $e'$ são concorrentes sse $e \nrightarrow e' \wedge e' \nrightarrow e$. Esta relação é representada por $e \parallel e'$. Nada se pode dizer (nem necessita ser dito) sobre a ordem em que estes eventos ocorrem.

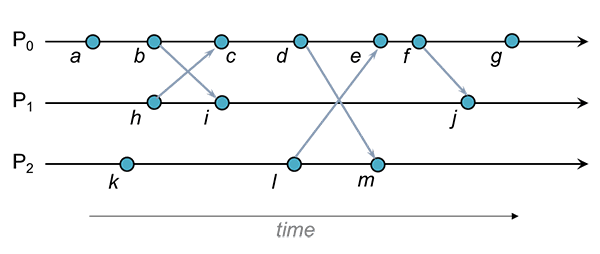
Exemplo

Algumas relações de antecedência encontradas no diagrama:

• $a \rightarrow b$
• $h \rightarrow c$
• $b \rightarrow j$
• $h \rightarrow m$

Algumas relações de concorrência encontradas no diagrama:

• $a \parallel l$
• $b \parallel h$

Relógio Lógico de Lamport

Leslie Lamport propôs um algoritmo simples para capturar a ordem de eventos num sistema distribuído. Cada processo $p_i$ mantém um relógio lógico monótono $L_i$ que pode ser usado para atribuir uma estampilha temporal $L_i(e)$ a cada evento $e$. Quando o processo em que se atribuiu a estampilha não é relevante, usa-se $L(e)$.

Os relógios são atualizados de acordo com as seguintes regras:

• LC1: $L_i$ é incrementado sempre que um evento é observado por $p_i$.
• LC2: Quando $p_i$ envia uma mensagem $m$, inclui na mensagem a estampilha $t$ com o valor de $L_i$ após executar LC1.
• LC3: Quando $p_i$ recebe uma mensagem $m$, atualiza $L_i$ tal que $L_i \coloneqq \max(L_i, t)$ e depois executa LC1.

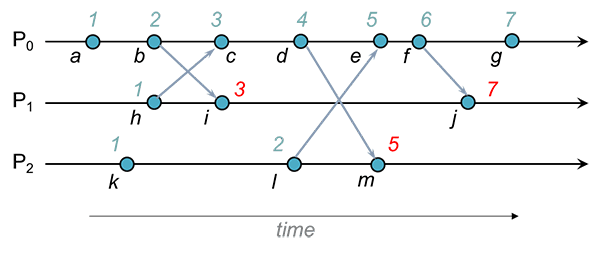
Exemplo

$P_0$, $P_1$ e $P_2$ mantêm, respetivamente, os relógios $L_0$, $L_1$ e $L_2$.

Quando $P_1$ envia a mensagem $m_{h \rightarrow c}$ inclui $t = 1$ na mensagem. Quando $P_0$ recebe a mensagem, compara $L_0$ com a estampilha recebida:

$$L_0 \coloneqq \max(L_0, t) + 1 = \max(2, 1) + 1 = 3$$

Quando $P_0$ envia a mensagem $m_{d \rightarrow m}$ inclui $t = 4$ na mensagem. Quando $P_2$ recebe a mensagem, compara $L_2$ com a estampilha recebida:

$$L_2 \coloneqq \max(L_2, t) + 1 = \max(2, 4) + 1 = 5$$

Relógios lógicos de Lamport garantem a seguinte propriedade:

No entanto, o inverso não é verdadeiro. Isto é, $L(e) < L(e') \nRightarrow e \rightarrow e'$. Pode-se encontrar um caso destes no exemplo anterior: $L(k) < L(c)$, mas $k \parallel c$.

Demonstração: $e \rightarrow e' \Rightarrow L(e) < L(e')$

Hipótese de indução: Se $e \rightarrow e'$, então $L(e) < L(e')$

Passo base (HB1): Se $e$ e $e'$ ocorrem no mesmo processo, é imediato por LC1 que $L(e) < L(e')$

Passo base (HB2): Se existe uma mensagem $m$ tal que $e$ é o evento de envio e $e'$ é o evento de receção, então $L(e) < L(e')$ por LC2 e LC3

Passo indutivo (HB3): Se $e \rightarrow e'$ e $e' \rightarrow e''$, então $L(e) < L(e')$ e $L(e') < L(e'')$, por HI $\square$

Vector Clocks

Para superar esta limitação, Mattern e Fridge desenvolveram o Vector Clock: uma alternativa em que garante também a implicação no sentido contrário.

O Vector Clock é um tuplo de $N$ inteiros, um para cada processo participante no sistema distribuído. À semelhança do relógio de Lamport, cada processo $p_i$ mantém um vector clock $V_i$ que pode ser usado para atribuir uma estampilha temporal $V_i(e)$ a cada evento $e$. Quando o processo em que se atribuiu a estampilha não é relevante, usa-se $V(e)$.

• VC1: Inicialmente, $V_i[j] = 0$ para todo o $i, j = 1, 2, ..., N$.
• VC2: $V_i[i]$ é incrementado sempre que um evento é observado por $p_i$.
• VC3: Quando $p_i$ envia uma mensagem $m$, inclui na mensagem a estampilha $t$ com o valor de $V_i$ após executar VC2.
• VC4: Quando $p_i$ recebe uma mensagem $m$, atualiza $V_i$ realizando um merge com $t$ e depois executa VC2.

A operação de merge dos vector clock $V_i$ e $t$ consiste em atualizar cada campo do vector clock $V_i$ tal que $V_i[j] \coloneqq \max(V_i[j], t[j])$, para todo o $j = 1, 2, ..., N$.

Uma possível intuição para estes valores é a seguinte:

• $V_i[i]$ é o número de eventos que $p_i$ estampilhou.
• $V_i[j]$ ($i \neq j$) é o número de eventos que $p_i$ já sabe que $p_j$ estampilhou.

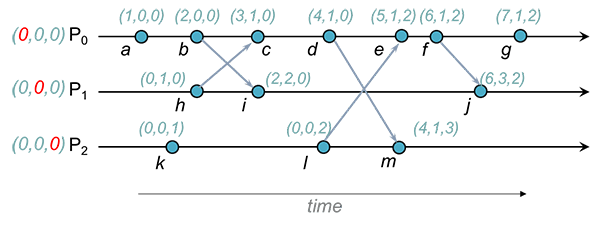
Exemplo

$P_0$, $P_1$ e $P_2$ mantêm, respetivamente, os relógios $V_0$, $V_1$ e $V_2$.

Quando $P_1$ envia a mensagem $m_{h \rightarrow c}$ inclui $t = (0,1,0)$ na mensagem. Quando $P_0$ recebe a mensagem, faz merge de $V_0$ com a estampilha recebida:

$$\begin{align} \nonumber V_0[0] &\coloneqq \max(V_0[0], t[0]) + 1 = \max(2, 0) + 1 = 3 \\ \nonumber V_0[1] &\coloneqq \max(V_0[1], t[1]) = \max(0, 1) = 1 \\ \nonumber V_0[2] &\coloneqq \max(V_0[2], t[2]) = \max(0, 0) = 0 \end{align}$$

Ou seja, $V_0 \coloneqq (3, 1, 0)$.

Quando $P_0$ envia a mensagem $m_{d \rightarrow m}$ inclui $t = (4, 1, 0)$ na mensagem. Quando $P_2$ recebe a mensagem, faz merge de $V_2$ com a estampilha recebida:

$$\begin{align} \nonumber V_2[0] &\coloneqq \max(V_0[0], t[0]) = \max(0, 4) = 4 \\ \nonumber V_2[1] &\coloneqq \max(V_0[1], t[1]) = \max(0, 1) = 1 \\ \nonumber V_2[2] &\coloneqq \max(V_0[2], t[2]) + 1 = \max(2, 0) + 1 = 3 \end{align}$$

Ou seja, $V_2 \coloneqq (4, 1, 3)$.

Pode-se comparar vector clocks da seguinte forma:

• $V = V' \Leftrightarrow V[j] = V'[j]$, para todo o $j = 1, 2, ..., N$.
• $V \leq V' \Leftrightarrow V[j] \leq V'[j]$, para todo o $j = 1, 2, ..., N$.
• $V < V' \Leftrightarrow V \leq V' \wedge V \neq V'$

Ou seja, temos que um vector clock é menor quando nenhum dos seus valores é maior, mas não são iguais. Comparando deste modo, obtemos a seguinte propriedade (uma versão da propriedade do relógio de Lamport mas com equivalência):

Demonstração: $e \rightarrow e' \Leftrightarrow V(e) < V(e')$

Começamos por mostrar que $e \rightarrow e' \Rightarrow V(e) < V(e')$

Hipótese de indução: Se $e \rightarrow e'$, então $V(e) < V(e')$

Passo base (HB1): Se $e$ e $e'$ ocorrem no mesmo processo, é imediato por VC2 que $V(e) < V(e')$

Passo base (HB2): Se existe uma mensagem $m$ tal que $e$ é o evento de envio e $e'$ é o evento de receção, então $V(e) < V(e')$ por VC3 e VC4

Passo indutivo (HB3): Se $e \rightarrow e'$ e $e' \rightarrow e''$, então $V(e) < V(e')$ e $V(e') < V(e'')$, por HI

De seguida, mostra-se que $V(e) < V(e') \Rightarrow e \rightarrow e'$

Para isto, prova-se que para um par de eventos $e$ e $e'$:

$$e \parallel e' \Rightarrow \neg(V(e) \leq V(e')) \wedge \neg(V(e') \leq V(e))$$

Seja $e$ e $e'$ um par de eventos concorrentes tal que $e$ ocorre em $p_i$ e $e'$ ocorre em $p_j$. Como os eventos são concorrentes, sabemos que nenhuma mensagem de $p_i$ durante ou após o evento $e$ propagou a sua estampilha para $p_j$ pelo momento em que ocorre $e'$, e vice versa.

Como $e$ ocorreu em $p_i$ e $p_j$ ainda não foi "informado", é garantido que $V_i[i] > V_j[i]$. Temos também que $V_j[j] > V_i[j]$. Provando-se assim o lema e o seu contra-recíproco:

$$V(e) \leq V(e') \lor V(e) \leq V(e') \Rightarrow \neg(e \parallel e')$$

Se dois eventos não são concorrentes, então tem de existir uma relação de happens-before, é evidente que $V(e) < V(e') \Rightarrow e' \rightarrow e$ é falso.

Logo, $V(e) < V(e') \Rightarrow e \rightarrow e'$ e temos que:

$$e \rightarrow e' \Leftrightarrow V(e) < V(e') \square$$

Referências

• Coulouris et al - Distributed Systems: Concepts and Design (5th Edition)
  • Secções 14.1, 14.2, 14.3 e 14.4
• Coulouris et al - Distributed Systems: Concepts and Design (5th Edition) - Instructor's Manual
  • Soluções dos exercícios 14.10, 14.11, 14.12 e 14.13
• van Steen and Tanenbaum - Distributed Systems
  • Secções 5.1 e 5.2
• Departamento de Engenharia Informática - Slides de Sistemas Distribuídos (2022/2023)
  • 3a Fundamentos: Tempo
• Paul Krzyzanowski - Assigning Lamport & Vector Timestamps
  • Imagens dos exemplos de eventos e relógios lógicos