Variáveis Aleatórias

Damos o nome de variável aleatória (VA) a qualquer função $X: \Omega \to \R^n$ que verifique uma condição de mensurabilidade.
Uma VA diz-se unidimensional se $n = 1$, bidimensional se $n=2$ e multidimensional se $n>2$.
O conjunto $X(\Omega) \subset \R^n$ é normalmente representado por $\R_X$.
Dizemos que uma VA é:

• discreta se $\R_X$ for contável;
• contínua se $\R_X$ não for contável;

Essencialmente, uma VA deve ser entendida como uma função que, para uma EA, traduz os resultados dessa EA. Vamos ver alguns exemplos:

Exemplo 1

Considere-se a experiência aleatória correspondente a lançar um dado ao ar. O espaço de resultados desta EA é o seguinte:

$$\Omega = \{ \text{Saiu 1}, \text{Saiu 2}, \text{Saiu 3}, \text{Saiu 4}, \text{Saiu 5}, \text{Saiu 6} \}$$

Uma variável aleatória que fará sentido é a função $X: \Omega \to \R$ tal que:

$$X(\text{Saiu 1}) = 1 \\ X(\text{Saiu 2}) = 2 \\ \cdots \\ X(\text{Saiu 6}) = 6$$

Agora já temos uma tradução da nossa experiência em números, pelo que podemos fazer continhas!!!

Exemplo 2

Considere-se a experiência aleatória que consiste em lançar um objeto ao ar e medir quanto tempo ele demora a cair ao chão. O espaço de resultados desta EA é

$$\Omega = \{ \text{O objeto demorou } x \text{ a cair}: x \in \R^+ \}$$

Uma variável aleatória que fará sentido definir é a função $X: \Omega \to \R$ tal que:

$$X(\text{O objeto demorou } x \text{ a cair}) = x$$

Exemplo 3

Considere-se a EA que consiste em lançar uma moeda ao ar. O espaço de resultados é:

$$\Omega = \{ \text{Sai Cara}, \text{Sai Coroa} \}$$

Uma VA que podemos definir é a função $X: \Omega \to \R$ tal que:

$$X( \text{Sai Cara} ) = 0 \\ X( \text{Sai Coroa} ) = 1$$

Condição de mensurabilidade

Dizemos que uma VA $X$ unidimensional tem uma condição de mensurabilidade se qualquer conjunto da forma $]-\infty, x]$ ($x \in \R$) tiver imagem inversa segundo $X$. Isto é, para qualquer conjunto $x \in \R$, existe um evento $A \in \Sigma$ tal que $X(A) = ]-\infty, x]$.

Para analisar probabilidades, atribuímos a VA's $X$ uma função de probabilidade $P: \Omega \to [0,1]$ definida por

Em relação a VA's, é também comum definir a função de distribuição (fd) como a função $F_X(x): \R \to [0,1]$ tal que

Dependendo se a VA é discreta ou contínua, esta função tem restrições e propriedades diferentes (apesar de análogas). Nomeadamente, para VA's discretas é possível usar somatórios, já que $\Omega$ é contável. Para VA's contínuas, por contraste, teremos de trabalhar com integrais.
Está, então, na altura de analisar cada caso em separado.

Variáveis Aleatórias Discretas

A função de probabilidade de uma VA discreta deve ser tal que:

• $P(X = x) > 0, \forall_{x \in \R_X}$
• $\sum_{x \in \R_X} P(X = x) = 1$

Para VA's discretas é evidente que a função de distribuição pode ser dada por

As VA's discretas satisfazem as seguintes propriedades:

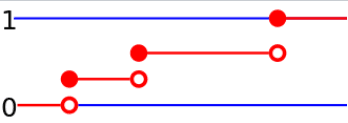
• $F_X$ é monótona crescente, contínua à direita e tem $\#\R_X$ pontos de descontinuidade. Consequentemente, o gráfico da fd de uma VA discreta é algo parecido a:

• $F_X(-\infty) = \lim_{x \to -\infty} F_X(x) = 0$;
• $F_X(+\infty) = \lim_{x \to +\infty} F_X(x) = 1$;
• $P(X < x) = P(X \leq x) - P(X = x) = F_X(x) - P(X = x)$;
• $P(X > x) = 1 - P(X \leq x) = 1 - F_X(x)$;
• $P(a < X \leq b) = F_X(b) - F_X(a)$;
• $P(a < X < b) = F_X(b) - F_X(a) - P(X = b)$;
• $P(a \leq X \leq b) = F_X(b) - F_X(a) + P(X = a)$;
• $P(a \leq X < b) = F_X(b) - F_X(a) + P(X = a) - P(X = b)$;

Variáveis Aleatórias Contínuas

Para VA's contínuas temos que qualquer evento elementar é impossível. Isto é:

Então, a melhor forma de caracterizar VA's contínuas é através da sua função de distribuição.
Dizemos, então, que uma VA $X$ é contínua se e só se:

• Possuir uma função de distribuição $F_X(x)$ contínua e crescente (em sentido lato) em $\R$;
• Existir uma função $f_X(x): \R \to \R_0^+$ tal que
  $$F_X(x) = \int_{-\infty}^x f_X(t) \, dt$$
  A esta função dá-se o nome de função de densidade de probabilidade (fdp).

As VA's contínuas têm as seguintes propriedades:

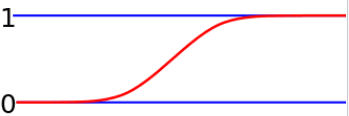
• Um gráfico vagamente semelhante ao representado abaixo, devido à continuidade e monotonia lata:

• $f_X(x) = \frac{\delta F_X(x)}{\delta x}$
• $F_X(-\infty) = 0$, $F_X(+\infty) = 1$ e, consequentemente, $0 \leq F_X(x) \leq 1$ para qualquer $x \in \R$;
• Para qualquer $a,b \in \R$:
  $$P(a < X < b) = P(a \leq X < b) = P(a < X \leq b) = P(a \leq X \leq b) = \\ F_X(b) - F_X(a) = \int_a^b f_X(x) \, dx$$

Valor Esperado e Variância

Por vezes, é relevante condensar informação sobre uma VA num só número. As funções mais que relevantes que nos dão informações sobre VA's são:

• Valor Esperado: $E(X)$, $\mu$ ou $\mu_x$
  É dado por:

  $$\begin{matrix} \text{Para VA's discretas} & & \text{Para VA's contínuas} \\ E(X) = \sum_{x \in \R_X} x P(X = x) & & E(X) = \int_{-\infty}^{\infty} x f_X(x) \, dx \\ \text{se esta série convergir} & & \text{se este integral convergir} \end{matrix}$$

  Definimos ainda o valor esperado de uma função $h$ sobre $X$ como:

  $$\begin{matrix} E(h(X)) = \sum_{x \in \R_X} h(x) P(X = x) & & E(h(X)) = \int_{-\infty}^\infty h(x) P(X = x) \\ \text{para } X \text{ discreta} & & \text{Para } X \text{ contínua} \end{matrix}$$

  Nomeadamente, se $h(x) = ax + b$, para $a, b \in \R$, verificamos que

  $$E(aX+b) = aE(X) + b$$

  Esta função é a medida de centralidade principal de uma VA.

• Variância: $Var(X)$, $V(X)$, $\sigma^2$ ou $\sigma^2_x$
  É definida como:

  $$V(X) = E\left( (X - E(X))^2 \right) = E(X^2) - E(X)^2$$

  A variância tem as seguintes propriedades:

  • $V(X) \geq 0$;
  • $V(X) = 0 \Leftrightarrow X$ constante;
  • $V(aX+b) = a^2V(x)$, para $a,b \in \R$.

  Esta função dá-nos uma medida de divergência em relação ao valor esperado (ao centro).

• Desvio Padrão: $DP(X)$, $\sigma$ ou $\sigma_X$
  É definido por:

  $$DP(X) = \sqrt{V(X)}$$

  Esta função tem a propriedade $DP(aX+b) = aDP(X)$.

  Esta função é usada principalmente quando se quer uma medida de desvio que funcione bem com multiplicações por escalares em $X$.