Memória

Tipos de Memória

Antes de falar de memória é importante apontar a diferença entre o CPU e RAM. A RAM é a memória primária enquanto que o processador faz os cálculos/computações. Pegando num exemplo, se tivermos um carpinteiro a arranjar uma cadeira e este tiver uma caixa com ferramentas, num dado momento só um certo número de ferramentas é que está a ser usado para consertar a cadeira. Estas ferramentas encontrar-se-ão mais próximas do carpinteiro, por exemplo no seu cinto, enquanto o resto estará na caixa. Usar as ferramentas que estão no seu cinto é mais rápido do que tirar uma ferramenta da caixa e usá-la. Se o carpinteiro for esperto, irá ter no seu cinto as ferramentas que precisa mais frequentemente para a tarefa que está a fazer no momento e deixará na caixa as ferramentas menos utilizadas. Assim, aplicando esta analogia a um computador, o carpinteiro é o CPU, as ferramentas que estão no cinto são a RAM e as ferramentas que estão na caixa são o disco rígido.

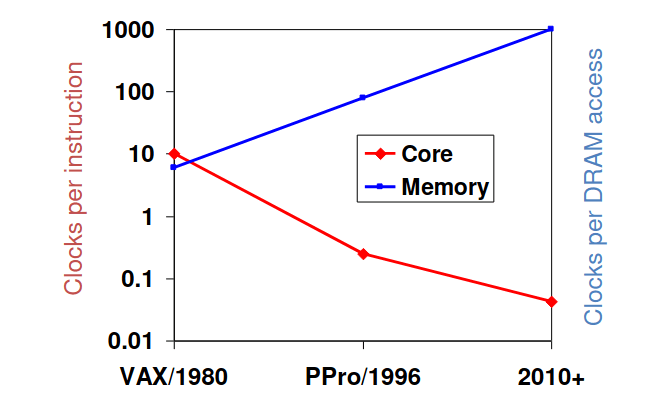
Nos últimos anos, a disparidade do aumento da velocidade dos processadores vs RAM tem vindo a aumentar, como se pode verificar na imagem seguinte:

Isto implica que o tempo de execução de um programa acaba por depender bastante mais na velocidade a que a RAM consegue enviar os dados para o CPU do que a velocidade do CPU. Portanto, mesmo que tenhamos o computador mais rápido do mundo com o mais recente processador, a sua velocidade vai estar limitada pela velocidade da nossa RAM. Isto significa que é necessário um bom design de hierarquia de memória e que este problema é cada vez mais importante. Mas quais são os diferentes tipos de tecnologias de memória?

Static RAM (SRAM), 0.5ns – 2.5ns, €1000 – €1000 per GB;
Dynamic RAM (DRAM), 50ns – 70ns, €10 – €20 per GB;
Flash memory, 5μs – 50μs, €0.5 – €1 per GB;
Magnetic disk, 5ms-20ms, €0.05 – €0.5 per GB;

Uma tecnologia de memória ideal teria, portanto, o tempo de acesso da SRAM, mas a capacidade e o custo/GB do disco magnético.

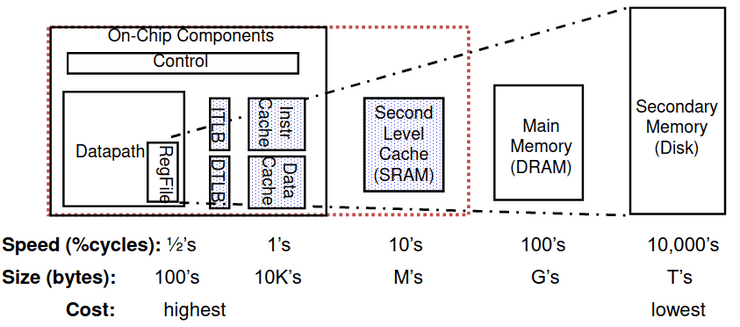
Típica Hierarquia de Memória

Tirando proveito do principio de localidade para mostrar ao utilizador o máximo de memória que há disponível na tecnologia mais barata à velocidade oferecida pela tecnologia mais rápida, temos:

Princípio da Localidade

O princípio da localidade, também conhecido como a localidade de referência, diz-nos que o programa de computador só requer acesso a uma percentagem muito pequena de espaço de memória a qualquer momento durante a execução.

SRAM	DRAM
usado por caches para velocidade e compatibilidade de tecnologia	usado pela memória principal para tamanho (densidade)
rápida (acesso típico demora 0.5 a 2.5 ns)	lento (acesso típico demora 50 a 70 ns)
densidade menor (6 células de transístores)	densidade maior (1 célula de transístor)
maior consumo (potência)	menor consumo (potência)
mais caro	mais barato
estático, o conteúdo fica para "sempre" enquanto estiver ligado	dinâmico, precisa de ser "refrescado" regularmente (a cada 8 ms); consome 1% a 2% dos ciclos ativos da DRAM

Para além disso, os endereços da DRAM são divídido em 2 metades, linha e coluna:

RAS (Row Access Strobe) que aciona o decodificador de linha;
CAS (Columm Access Strobe) que aciona o selecionador de coluna.

Como Funciona a Hierarquia de Memória?

É importante sabermos como, e porquê, a hierarquia de memória funciona.

O desenho desta hierarquia tem em mente dois grandes princípios: o princípio de localidade temporal e o de localidade espacial.

A localidade temporal pressupõe que se uma certa localização de memória é referenciada num dado instante, então é bastante provável que volte a ser referenciada outra vez em breve.
Um exemplo disto são variáveis dentro de um loop, que são referenciadas várias vezes durante a execução do mesmo.

A localidade espacial pressupõe que se uma localização de memória for referenciada, então é bastante provável que os endereços vizinhos sejam referenciados em breve.
Um exemplo disto é o acesso a vetores/arrays.

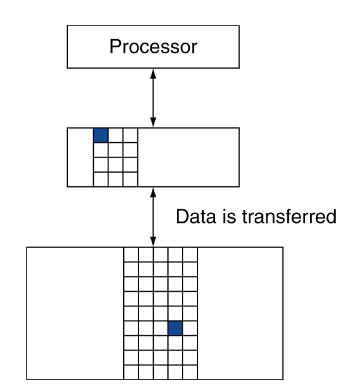
Assim, ao termos uma hierarquia de memória, vamos guardando tudo no disco, copiamos os items recentemente acedidos (e mais próximos) do disco para a memória DRAM mais pequena (memória principal) e por último copia estes items do DRAM para uma memória SRAM mais pequena (memória cache) que está conectada ao CPU.

Níveis de Hierarquia de Memória

Como podemos ver na imagem acima, dentro da memória existem vários níveis que a ajudam a trabalhar como deve. Por vezes a memória pode estar agrupada em blocos (linhas), que é a unidade que é copiada entre níveis da hierarquia, e que pode ser composta por várias palavras.

Se tentarmos aceder a dados e estes estiverem disponíveis no nível mais alto da hierarquia, temos um hit, caso contrário teremos um miss e teremos de ir buscar os dados a um nível inferior.

Podemos ainda calcular o hit rate de multiplos acessos através da seguinte fórmula:

\op{\text{Hit Rate}} = \frac{\text{Hits}}{\text{Accesses}}

Quando ocorre um miss, o bloco é copiado para um nível mais baixo e os dados acedidos são fornecidos de um nível superior. Temos, portanto, tempo perdido a repôr o bloco nesse nível, chamado miss penalty, com o bloco de nível inferior correspondente.

Podemos calcular o ̣miss rate através da seguinte fórmula:

\op{\text{Miss Rate}} = \frac{\text{Misses}}{\text{Accesses}} = 1- \text{Hit Rate}

O hit time é equivalente ao tempo de acesso ao bloco num certo nível, mais o tempo que é necessário para determinar se ocorre um hit/miss.
Podemos, portanto, inferir, que o nosso hit time é, geralmente, muito inferior ao miss penalty.

Memória Cache

A memória cache corresponde ao nível de hierarquia de memória mais perto do CPU.

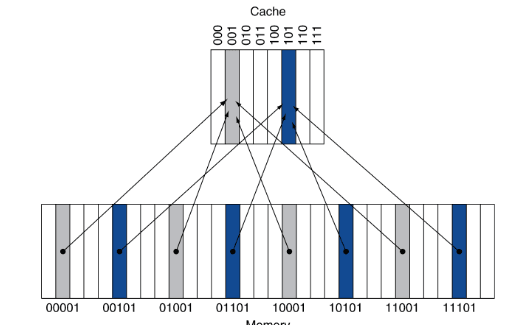
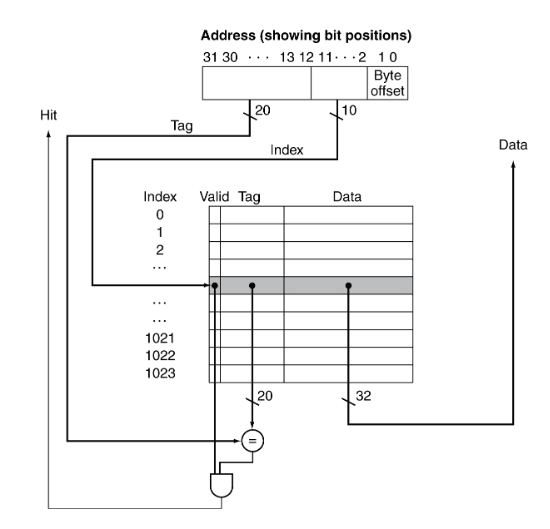
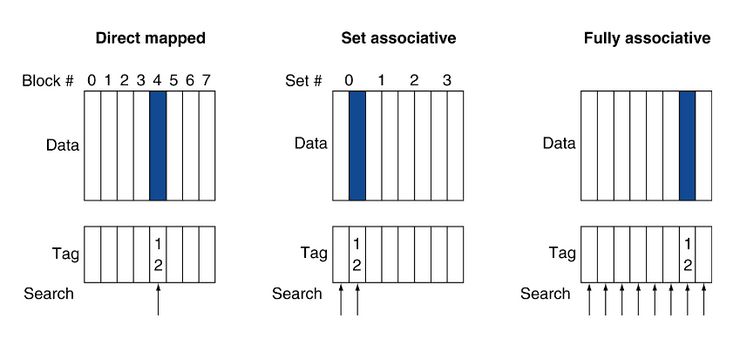
Mapeamento Direto

Uma das formas de organizar a cache é o mapeamento direto. Este método define que cada endereço de memória está associado a um, e apenas um, índice na cache.

Analogia

Imaginemos que temos 10 cadeiras onde se podem sentar alunos do Técnico. No entanto, cada aluno só se pode sentar na cadeira que corresponde ao último dígito do seu número de aluno.

O que acontece se os alunos 99211 e 99311 se quiserem ambos sentar nas cadeiras?
Não dá! Ambos os alunos teriam de se sentar na mesma cadeira, o que não é possível. Mesmo que existam outras cadeiras disponíveis, estes alunos só estão autorizados a sentar-se na cadeira 1.

O que acontece é que quando um se quer sentar, o outro tem de ceder o lugar.

É assim que funcionam as cache de mapeamento direto: cada endereço na memória está associado a um índice na cache (definido por um certo conjunto de bits no seu endereço), e quando este é colocado em cache, quaisquer dados que já lá estejam têm de ser descartados, mesmo que existam outros blocos livres.

Esta é a forma mais simples de mapeamento. A posição do bloco na cache depende do seu endereço na memória principal, pelo que cada palavra possui uma posição (index) fixa.

Mas como é que sabemos se um bloco em particular está guardado na cache? Afinal de contas, existem vários endereços que podem estar presentes no mesmo índice. Quando guardamos o bloco na cache, guardamos também o restante do endereço. A isto chamamos tag. Quando queremos verificar se um endereço está guardado em cache, vamos ao índice correspondente e comparamos a tag guardada com a tag do endereço a que queremos aceder. Se corresponderem, o bloco em cache é o bloco a que queremos aceder.
Além disso poderemos ter de testar se o valid bit está ativo (1), caso contrário a entrada em cache apenas contém "lixo".

Exemplos de cache

Para exemplos de como trabalhar com exercícios de caches é recomendada a resolução das fichas práticas.

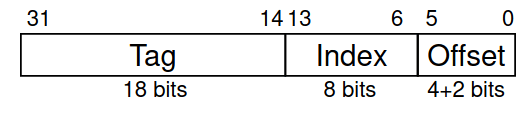
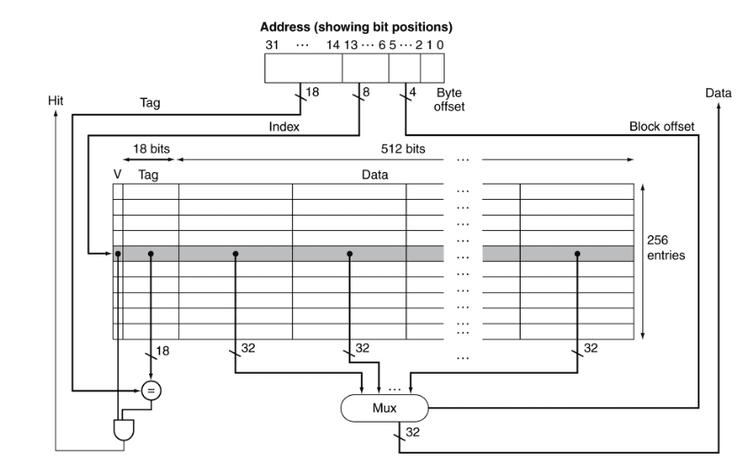
Tamanho de Blocos

Se tivermos 256 blocos com 16 palavras por bloco, como é que podemos descobrir qual é o bloco que o endereço 19200 (em decimal) mapeia?

Começamos por remover o offset, que podemos fazer ao dividir por $2^{2+4}$ .

\frac{19200}{2^{2+4}} = 300

Agora que já removemos o offset, podemos calcular o nosso número de bloco (índice)! Sabendo que o índice ocupa 8 bits, podemos fazer

300 \op{mod} 2^8 = 44

que nos dá o índice.

Podemos por isso concluir que blocos maiores deviam reduzir o miss rate devido à localidade espacial. No entanto, numa cache de tamanho fixo, blocos maiores implicam menos blocos, o que pode resultar num miss rate mais elevado. Além disso, blocos maiores também implicam um maior miss penalty, dado que demoram mais tempo a ser transferidos. Iremos mais à frente ver políticas de escrita que podem atenuar estas desvantagens.

Por esta razão, é preciso encontrar um ponto de equilíbrio entre tamanho do bloco e miss rate.

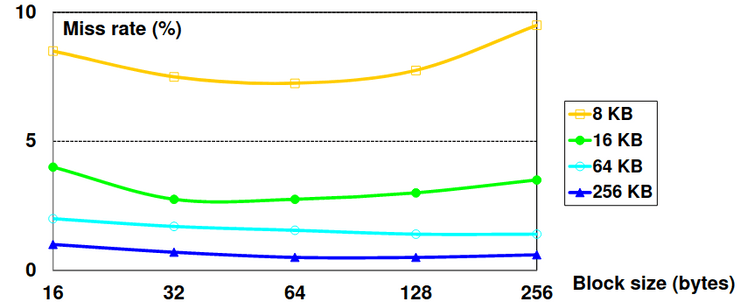
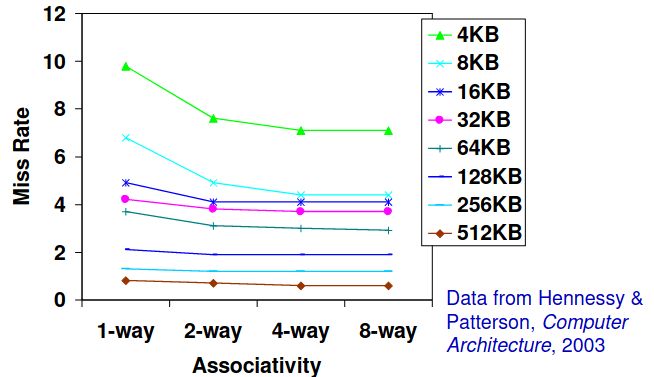
Miss Rate vs Block Size vs Cache Size

Como podemos ver no gráfico acima, a miss rate sobe quando o tamanho do bloco ocupa uma fração mais significativa do tamanho da cache, visto que o número de blocos que podem estar contidos simultaneamente na cache é menor. Isto resultará num aumento de capacity misses.

Melhorar a Performance da Cache

Conteúdo Não Revisto

O conteúdo abaixo não foi revisto e poderá conter erros. Agradecem-se contribuições.

Apenas foi aqui incluído devido à proximidade do MAP45 dia 2022-10-20.

Começamos por avaliar um exemplo: Intrinsity FastMATH, que corresponde a uma série de microprocessadores desenvolvidos pela Intrinsity utilizando a tecnologia Fast14, isto é, processadores que usam a domino logic dynamic. Estes chips incorporados no núcleo do FastMIPS juntamente com uma matriz de performance muito elevada e um coprocessador de matemática vetorial.

Vendo a um nível mais interior, sabemos que a Intrinsity tem um processador MIPS embebido com uma pipeline de 12 estados e instruções assim como acesso a data em cada ciclo. Dentro da cache, temos uma cache dividida, separada em cache I e cache D, cada um tamanho de 16KB (256 blocks cada um com 16 palavras), e a cache D com write-through ou write-back. Em termos de SPEC2000 miss rates, temos:

Cache I: 0.4%;
Cache D: 11.4%;
Weighted average: 3.2%

Cache Misses

Mas o que são estas cache misses? Quando um sistema or aplicação faz um pedido para receber dados da cache, mas esses dados especificamente não se encontram na memória cache, temos uma cache miss. Isto implica que a pipeline do CPU para, vai buscar um bloco ao próximo nível de hierarquia, temos que dar restart à busca de instruções e como há data cache miss à um acesso a dados completo. Estes dependem de padrões de acesso a memória, algoritmos de comportamento e otimização do compilador para acessos a memória.

Existem três tipos de cache misses:

Compulsory: também conhecidas por cold start misses ou first references misses, estes misses acontecem quando há um primeiro acesso a um bloco que tem que ser trazido para a cache;
Capacity: este tipo de misses acontecem quando o working set de um programa tem uma capacidade muito maior que a cache; visto que a cache não consegue conter todos os blocos que são necessários para a execução do programa, a cache é obrigada a descartar estes blocos;
Conflict: também conhecidos como collision misses ou interference misses, estes ocorrem quando um número elevado de blocos são mapeados para o mesmo set ou block frame, num set de associatividade ou até mesmo em posicionamento de blocos em mapeamento direto.

Write-Policies

Uma write policy da cache refere-se a um comportamento da cache enquanto está a tratar de alguma operação. Este tem um papel muito importante numa variedade de características diferentes expostas pela cache. Vendo agora mais aprofundadamente os tipo de cache, começamos por analisar os três tipos de write policies.

Write-through

Quando nos deparamos com um data-write hit podemos somente atualizar o bloco da cache, mas isto implicaria que a cache e a memória se tornassem insconsistentes. Temos, por isso, que introduzir a política write-through: esta, sendo a mais fácil de implementar, basicamente atualiza os dados tanto em cache como em memória ao mesmo tempo. É usada quando não há escritas muito frequentes na cache e ajuda com a recuperação de dados.

Contudo, temos um atraso visto que estamos a escrever em duas localizações. Assim, temos que inserir um buffer de escrita que consegue guardar os dados que estão à espera para serem escritos em memória, dando possibilidade ao CPU de continuar imediatamente, apenas atrasando na escrita se o buffer estiver cheio.

Write-back

Quando os dados são atualizados apenas em memória e em cache só é atualizada mais tarde, temos a política write-back. Os dados são atualizados em memória somente quando a linha da cache está pronta para ser trocada, o que significa que a atualização do armazenamento acontece assincronamente numa sequência à parte! É possível começar uma sequência de diferentes maneiras antes do retorno da nossa resposta, periodicamente ou integrada na cache baseado numa entrada da cache chamada dirty state. Quando este é trocado, voltamos a escrever em memória e podemos usar um buffer para permitir a troca de blocos que têm que ser lidos primeiro.

Write-allocation

Vimos as possibilidades de acontecimentos quando há sucesso em termos de escrita em cache e na memória, mas o que acontece quando falha? Nestes casos temos um write-around. Se não estamos à espera de uma operação de escrita pouco depois dos dados de leitura terem sido acedidos, a cache começa a ficar poluída com entradas que não estão a ser usadas; de modo a impedir que tal aconteça, podemos desviar a alocação em caso de cache miss.

Desta forma, em alternativa ao write-through podemos alocar em caso de miss, indo buscar o bloco, ou ter um write-around onde não vamos buscar o bloco. Por último em caso de write-back, costumamos ir buscar o bloco.

Loading Policies

Agora que já vimos como é que podemos escrever num bloco, temos também que ver como podemos carregar um bloco. Este pode ser feito de três formas diferentes:

Blocking: a palavra requisitada é mandada para o processador a seguir ao bloco inteiro ter sido carregado na cache; é mais fácil de implementar mas segundo a localidade espacial, o próximo acesso tem que ser do mesmo bloco;
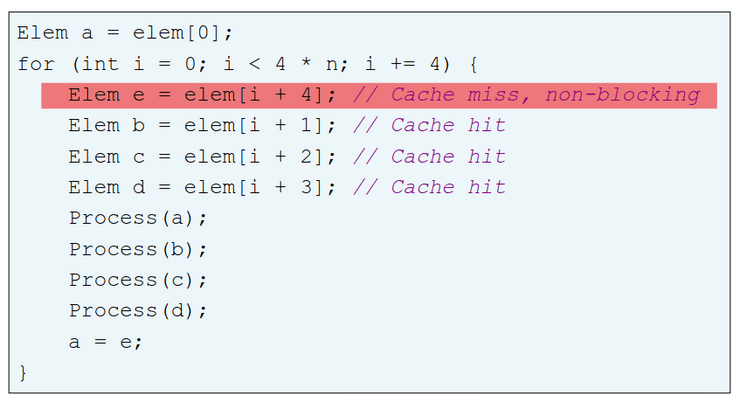
Non Blocking: tem um maior impacto nas caches onde o bloco carregado implica vários acessos a memória:
- Early restart: vai buscar palavras em ordem normal, mas assim que a palavra requisitada chega ao bloco, é mandada para o processador e permite que este continue a sua execução;
- Critical Word First: a palavra em falta é requisitada primeiro em memória e mandada para o processador assim que esta chega; isto deixa que o processador continue a sua execução enquanto preenche o resto das palavras no bloco.

Medir a Performance da Cache

Para conseguirmos perceber se uma cache está a funcionar bem ou não, temos que saber os termos involvidos nestes cálculos:

Bloco ou linha: a unidade mínima de informação que está presente, ou não, na cache;
Hit-rate: a fração de memória acedida encontrada num nível de hierarquia de memória;
Miss-rate: a fração de memória acedida não encontrada num nível de hierarquia de memória. Pode ser dada através de $1- \text{Hit Rate}$ ;
Miss penalty: tempo que demora a repôr um bloco num nível com o bloco correspondente num bloco num nível inferior.

Assim, como já sabíamos, os componentes do tempo do CPU são os ciclos de execução do programa, que includem o tempo de cache-hit e os ciclos de atraso de memória que provêm maioritariamente de cache misses. Assumindo que o sucesso de cache incui a parte normal dos ciclos de execução do programa, então podemos calcular o tempo de CPU através da seguinte fórmula:

\text{CPU time} = IC \times CPI \times CC = IC \times (CPI_\text{ideal} + \text{Memory-stall cycles}) \times CC

Sabendo que o que está entre parêntesis corresponde ao $CPI \times \text{stall}$ . Assumindo, também que os miss rates de escrita e lida estão juntos, podemos calcular a memory-stall cycles através da seguinte fórmula:

\text{Memory-stall cycles} = \text{accesses/program} \times \text{miss rate} \times \text{miss penalty}

Da mesma forma, para calcularmos o tempo médio de acesso (AMAT- average memory access time), temos a seguinte fórmula:

\text{AMAT} = \text{hit time} + \text{miss rate} \times \text{miss penalty}

Exemplo

Analisando melhor o que acabámos de ver, imaginando que temos uma cache I com um miss rate de 2% e uma cache D com um miss rate de 4%, assim como um miss penalty de 100 ciclos, uma base CPI, ou seja, cache ideal, igual a 2, e loads e stores que ocupam 36% das instruções.

A primeira coisa que pretendemos calcular são os miss cycles por instrução, que, como vimos aicma, são dados pelo miss rate e o miss penalty. Temos, por isso:

\text{miss cycle} = \text{miss rate} \times \text{miss penalty}

\text{I-cache} = 0.02 \times 100 = 2

\text{D-cache} = 0.36 \times 0.04 \times 100 = 1.44

Logo. o verdadeiro CPI pode ser dado através de:

\text{CPI} = 2 + 2 + 1.44 = 5.44

Por isso. o CPU ideal é $5.44/2=2.72$ vezes mais rápido

Ideias a Reter

Desta forma, concluimos que quando a performance do CPU aumenta, o miss penalty diminui; uma diminuição baseada no CPI implica uma maior proporção de tempo gasto em atrasos na memória; e, um aumento de clock rate significa que os atrasos de memória contam para mais ciclos de CPU. Não podemos, evidentemente negligenciar o comportamneto da cache quando estamos a avaliar a perfomance do sistema.

Reduzir os Miss Rates na Cache

Uma forma muito útil de evitarmos ter tantas falhas quando vamos à cache, é através de caches associativas. Estas dão uma maior liberdade ao posicionamento de blocos, sendo que numa cache de mapeamento direto um bloco de memória mapeia para exatamente um único bloco de cache e, no outro extremo, podemos permitir que um bloco de memória seja mapeado para qualquer bloco de cache numa cache totalmente associativa.

Por isso mesmo, o compromisso é dividir a cache em sets que contêm n formas (n-way set associative). Os blocos de memória mapeiam um set único, específicado pelo campo de index, e pode ser posto em qualquer sítio desse set, é por isso que há n escolhas.

Totalmente associativo	Associatividade com n sets
Contém um set	Contém n entradas em cada set
Autoriza um bloco para ir a qualquer entrada na cache	O número do bloco determina o set
É obrigátorio procurar em todas as entradas de uma só vez	Procura todas as entradas de um determinado set de uma vez
Comparador por cada entrada (mais caro)	N comparadores (mais barato)

Exemplo

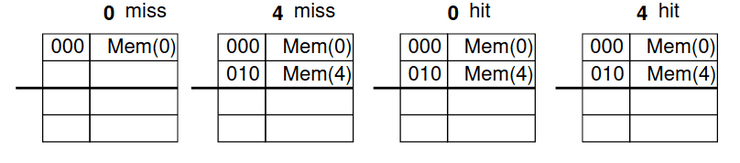
Imaginando que a referência da memória da palavra principal corresponde à string 0 4 0 4 0 4 0 4 e que começamos com uma cache vazia, tem-se:

Começando pelo primeiro número, ou seja o 0, nós vamos à cache e vemos se o valor 0 se encontra presente. Como não se encontra, temos um miss e escrevemos na primeira linha o valor 0. Já tendo o 0 em cache, seguimos para o 4, vamos à primeira linha e vemos se está na cache, contudo na cache só está o 0, logo, há um miss. Como estamos a tratar do número 4, contamos as linhas até chegarmos à linha 4, como só há 4 linhas no total e começamos a contar do zero, temos que modficar a nossa primeira linha para passar a ter a informação relevante ao 0 para ter informação relevante ao 4. Assim, na nossa primeira linha agora temos o 4.

Acabando os dois primeiros valores, passamos ao 0, vamos à primeira linha, vemos que já está preenchida, há miss e temos que voltar a preencher com o 0. Reparamos, por isso, que temos o mesmo caso que no início do nosso exercício. Ora, como o resto dos valores são sempre ou 0 ou 4 intrecalando, vamos sempre ter um miss e vamos sempre ter que voltar a preencher a primeira linha com o valor 0 ou 4.

Porém, se tivessemos a ver a mesma string mas numa 2 way set associative_cache, só teríamos miss nos primeiros dois acessos, visto que os nossos valores seriam guardados na primeira e segunda via da primeira linha, e a partir daí conseguiríamos aceder aos endereços 0 e 4 com sucesso.

Porém, nem sempre nos dá mais jeito termos associatividade de sets: esta escolha depende do custo do miss comparado com o custo da implementação, como podemos ver no gráfico abaixo, nem sempre quanto maior é a nossa associatividade menos misses há!

Política de Troca

Agora que já sabemos que há alturas em que temos que ir mudando os valores que estão nas nossas caches, como é que podemos escolher quais são os valores que eliminamos para dar acesso a novos? Em mapeamento direto não temos escolha, contudo num set de associatividade geralmente vemos primeiro se há alguma entrada não válida, se não escolhemos a entrada que não está a ser usada há mais tempo (LRU- least-recently used), o que é simples para uma via de 2, é gerível com facilidade para 4, mas mais do que isso é demasiado díficil; nesses casos funciona mais ou menos da mesma forma mas mais aleatório.

Exemplos

Para mais exemplos de como aceder à cache e ir trocando os elementos é recomendada a realização da quarta ficha das aulas práticas ou ver a sua resolução.

Cache Vítima

Em vez de descartar completamente cada bloco quando estão a ser repostos, podemos mantê-lo temporariamente num buffer vítima, ou seja, quando o bloco saí vai sempre para a cache vítima e é completamente associativa, dando a ilusão que estamos a tratar com uma maior associatividade do que realmente estamos.

Assim, em vez de parar um subsequente miss à cache, os conteúdos do buffer são vistos quando há um miss para ver se estão aí os dados pretendidos antes de ir a um nível de memória inferior. Esta cache é mais pequena, contendo apenas 4 a 16 posições, totalmente associativa, e particularmente eficiente para pequenos mapeamentos diretos a caches: mais de 25% de redução no número de misses numa cache de 4kB.

Caches de Níveis Múltiplos

Outra forma de reduzir o miss rate da cache é através de níveis múltiplos de cache. Com o avanço da tecnologia, temos mais espaço para ter uma cache L1 maior, ou ter um segundo nível de cache L2 unificado. É importante referir que podemos ter mais níveis de cache mas que para já não é necessário considerá-los.

Contudo, estas caches têm considerações de design muito diferentes. Enquanto a cache primária que está conectada ao CPU foca-se em minimizar o hit time com blocos mais pequenos, a cache de nível dois serve para os misses da cache primária, focando-se em reduzir o miss rate através da redução da penalidade de tempos de acesso à memória longos, tendo por isso tamanhos de blocos maiores e mais níveis de associatividade.

Isto significa que a cache L1 tem um tamanho menor que uma cache única, assim como um tamanho de blocos menor que os blocos da cache L2. Assim, para calcularmos os tempos de acesso, seja t de tempo e p de probabilidade, temos que usar a fórmula:

t_\text{access} = t_\text{hitL1} + p_\text{missL1} \times t_\text{penaltyL1}

t_\text{penaltyL1} = t_\text{hitL2} + p_\text{missL2} \times t_\text{penaltyL2}

t_\text{access} = t_\text{hitL1} + p_\text{missL1} \times (t_\text{hitL2} + p_\text{missL2} \times t_\text{penaltyL2})

Se não houver cache L2, L1 é o único tempo de acesso à memória.

Example

Se tivermos um CPU base CPI igual a 1, um clock rate de 4GHz, miss rate/instruction de 2% e tempo de acesso à memória principal 100 ns, apenas com a memória principal, teríamos de calcular a efetividade do CPI da seguinte forma:

\text{Miss penalty} = 100ns/0.25ns = 400 \text{ cycles}

\text{Effective CPI} = 1 + 0.02 \times 400 = 9

Sabendo que na primeira equação estamos a dividir o tempo de acesso à memória pelo inverso do clock rate, e na segunda equação estamos a somar o CPU base CPI à multiplicação entre o miss rate e o número de ciclos calculado na equação anterior.

Porém, se tivermos uma cache L2 com tempo de acesso de 5ns e um miss rate global para a memória principal de 0,5%, já calcularíamos o CPI de forma diferente, ou seja:

\text{Penalty} = 5ns/0.25ns = 20 \text{ cycles}

\text{Extra penalty} = 400 \text{ cycles}

\text{CPI} = 1 + 0.02 \times 20 + 0.05 \times 400 = 3.4

Assim, podemos inferir que o nosso rácio de performance vai ser $9/3.4=2.6$ vezes maior com uma cache.

Otimização de Código

O objetivo principal é reduzir o miss rate através da mudança de padrões de acesso a memória com técnicas de otimização de código. Para tal, temos que considerar maioritariamente misses de conflito assim como acessos a dados e a programas. Geralmente, há uma maior flexibilidade a reorganizar os dados em memória e os seus padrões de acesso correspondentes.

Existem várias técnicas para otimização de acesso de dados:

Pré-busca e pré-carregamento de dados na cache;
Esquema de estrutura que seja consciente em termos de cache:
- reorganização do campo, geralmente agrupados conceptualmente;
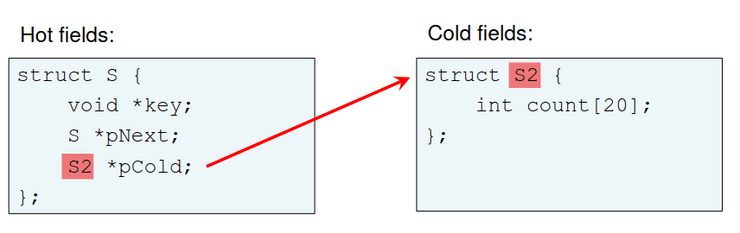
- Hot/cold splitting
Estruturas de dados em árvore;
Linearização de caching;
Alocação de memória;
Bloqueamento e mineração a céu aberto;
Preenchimento de dados para alinhar as linhas da cache;
entre muitos outros...

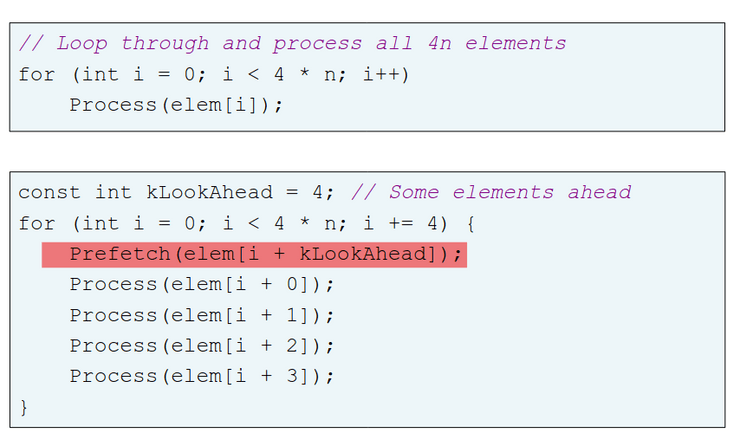
Pré-busca e Pré-carregamento

Pré-busca, prefetching em inglês, refere-se ao carregamento de um recurso antes que seja necessário de modo a diminuir o tempo de espera para esse recurso. Assim, um software prefetching não pode ser feito nem demasiado cedo, visto que os dados podem ser expulsos antes de serem usados, nem demasiado tarde pois os dados podem não der trazidos a tempo da sua utilizção. Esta técnica é greedy. Da mesma forma, o pré-carregamento, ou preloading em inglês funciona como um pseudo prefetching, usando um processamento hit-under-miss, isto é o acesso antigo é um miss e, por isso, o acesso seguinte será um hit.

Prefetching:

Preloading:

Greedy Prefetching:

Estruturas

Como já vimos acima, podemos ter um esquema que sej cache-conscious, e por isso podemos ter uma reorganização de campo, field reordering, ou um hot/cold splitting, que podem ser representados da seguinte forma.

Field reordering

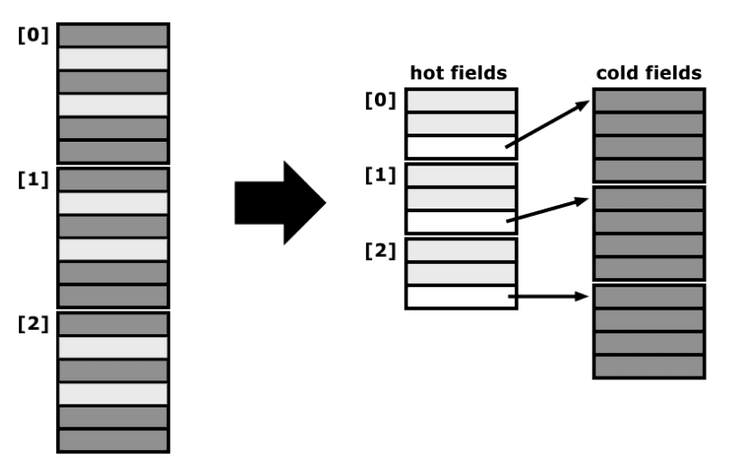
Um hot/cold splitting permite alocar toda a estrutura "S" da piscina de memória, aumentando a coerência, e tem preferência por uma alocação parecida com um array, não sendo necessário pointers a sério para os campos frios, como podemos ver no esquema abaixo.

Hot/cold splitting

Merging Arrays

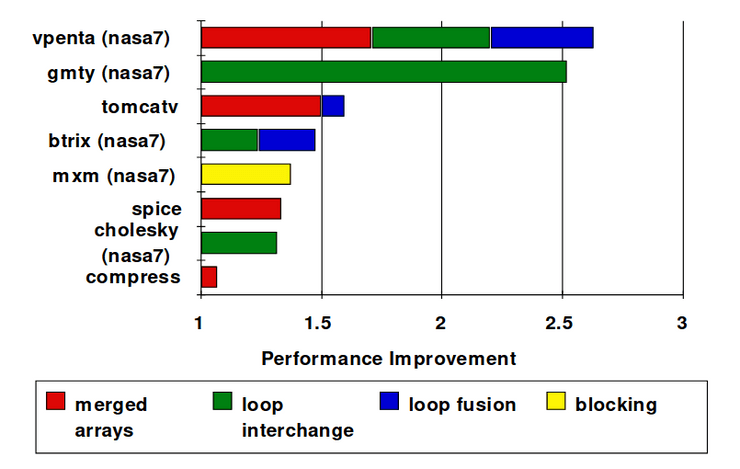
Em 1989, McFarling reduziu cache misses por 75% em caches de mapeamento direto de 8 kB e blocos de 4 bytes em software. Para tal, foi necessário reorganizar os procedimentos em memória para reduzir os conflict misses, assim como fazer um perfil de modo a analizar os conflitos, usando ferramentas que eles desenvolver. Os dados obtidos foram os seguintes:

Merging arrays: melhoram a localidade espacial através de um único array de elementos compostos vs dois arrays;
Loop fusion: combinam dois loops independentes que têm o mesmo looping e alguma sobreposição de variáveis;
Loop interchange: mudam o nesting dos loops para terem acesso a dados em ordem de memória guardada;
Blocking: melhoram a localidade temporal através do acesso a "blocos" de dados repetidamente vs descer colunas e linhas inteiras.